วงจรลอจิกแบบคอมไบเนชั่น

ในหัวข้อที่ผ่านมา เราได้รู้จักถึงเกตพื้นฐานชนิดต่างๆ และ พีชคณิตของบูลีนที่ช่วยในการอธิบายการดำเนินการของวงจรให้อยู่ในรูปนิพจน์และวิเคราะห์การทำงานของวงจรที่สร้างจากวงจรลอจิกเกตหลายๆแบบมาต่อรวมกันหรือ เรียกว่าเป็นวงจรแบบคอมไบเนชั่น (Combination) วงจรคอมไบเนชั่น นี้ไม่มีลักษณะของความจำ (Memory) เอาต์พุตของวงจรคอมไบเนชั่น ขึ้นอยู่กับอินพุตในขณะนั้นๆ

1. ผลบวกของผลคูณ (Sum-of-Product)

            ในการลดรูปวงจรลอจิก เราจะต้องการเรียนรู้การเขียน นิพจน์ในรูปของผลบวกของผลคูณ

          

ความหมายของผลบวกของผลคูณคือ เทอมของการแอนด์หลายๆเทอม ออร์กัน โดยที่เทอมแอนด์แต่ล่ะเทอมอาจมีตัวแปรอยู่ในรูปคอมพลีเมนต์หรือ อยู่ในรูปที่ไม่เป็นคอมพลีเมนต์ (ไม่กลับผลลอจิก) เพียงเท่านั้น

 หมายเหตุจะไม่เครื่องหมายนิเสธครอบบนตัวแปรมากกว่าหนึ่งตัว (เช่นหรือเป็นต้น )         

2. ผลคูณของผลบวก (Product-of-Sum)

            รูปแบบทั่วไปอีกชนิดหนึ่งคือ ผลคูณของผลบวก ที่ประกอบไปด้วยเทอมออร์หลายๆเทอม แอนด์กันอยู่

ในการลดรูปเราสามารถใช้นิพจน์ในรูปผลบวกของผลคูณแต่เพียงอย่างเดียวได้ ดังนั้น จะไม่กล่าวถึงการลดรูปโดยการใช้รูปผลคูณของผลบวก

3. การลดรูปวงจรลอจิก

            เมื่อเราสามารถเขียนนอพจน์ของเอาต์พุตของวงจรลอจิกขึ้นมาได้ เราอาจจะสามารถลดรูปให้เป็นนิพจน์ใหม่ที่มีจำนวนเทอม หรือ จำนวนตัวแปรลดลง ซึ่งทำให้เราใช้จำนวนเกตที่ลดลงด้วย ทำให้วงจรมีขนาดเล็กลงและราคาถูกลง นอกจากนี้ความเชื่อมั่นของวงจรก็จะมีสูงขึ้นเนื่องจากมีจำนวนจุดต่อที่ลดลง

4. การลดรูปโดยวิธีทางพีชคณิต

            เราสามารถใช้ทฤษฎีบทของบูลีนในการลดรูปนิพจน์สำหรับสร้างวงจรลอจิก เป็นการยากที่จะระบุว่าควรใช้ทฤษฎีบทของบูลีนข้อใด ในการลดรูปนิพจน์ ให้อยู่ในรูปที่ง่ายที่สุด เพราะขึ้นอยู่กับการลองผิดลองถูกและความชำนาญของเฉพาะบุคคล ในตัวอย่างต่อไปจะแสดงวิธีการลดรูปนิพจน์หลายๆวิธี ซึ่งจะสังเกตได้ว่ามีขั้นตอนสำคัญๆ  2 ขั้นตอนคร่าวๆได้ดังนี้

1. ทำการแปลงนิพจน์ตั้งต้นให้อยู่ในรูปผลบวกของผลคูณ โดยใช้ทฤษฎีบทของ ดีมอร์แกนและการคูณเทอม

2. เมื่อสามารถแปลงให้อยู่ในรูปของผลบวกของผลคูณได้แล้ว จึงพิจารณาหาเทอมที่มีร่วมกัน แล้วทำการดึงเทอมร่วมนั้นออกมา เพื่อหวังให้จำนวนเทอมลดลง

ตัวอย่าง จงลดรูปวงจรลอจิกต่อไปนี้

วิธีทำ

ขั้นตอนแรกให้หานิพจน์ของเอาต์พุต z ของวงจรลอจิก

ผลลัพธ์ที่ได้นี้เมื่อนำมาสร้างเป็นวงจรลอจิกในรูปที่ 4.1(b) จะเห็นได้ว่ารูปวงจรมีความซับซ้อนน้อยลงเป็นอย่างมาก

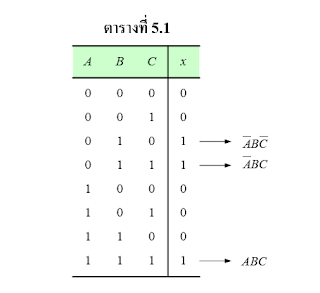
5. การออกแบบวงจรลอจิกคอมไบเนชั่นจากตารางความจริง

            ตัวอย่าง5.1 จงออกแบบวงจรลอจิกที่มีตารางความจริง ในตารางที่ 5.1

6. การลดรูปวงจรโดยการใช้ Karnaugh Map

            Karnaugh map เป็นวิธีทางภาพที่ใช้ในการลดรูปสมการลอจิก ในทางปฎิบัติ สามารถใช้กับตัวแปรบูลีนได้สูงสุด 6 ตัวแปร สำหรับการสร้างตารางด้วยมือจะจำกัดที่ 4 ตัวแปร

ตัวอย่างตารางสำหรับ 2 ตัวแปร 3 ตัวแปร และ 4 ตัวแปร แสดงไว้ในรูปที่ 6.1

การจับคู่เทอมที่เหมือนกัน สามารถทำได้โดยการวงรอบเทอมที่อยู่ติดกัน เป็นแบบ 2 เทอม 4 เทอม และ 8 เทอม โดยเทอมที่ตัวแปรในรูปคอมพลีเมนต์และรูปปกติจะถูกยุบไป

6.1 วงรอบ 2 เทอม

พิจารณาตัวอย่างการวงรอบเทอมที่อยู่ติดกันสองเทอม

7. Exclusive-OR และ Exclusive-NOR

            วงจรลอจิกเกตแบบพิเศษที่นิยมใช้ในระบบดิจิตอลคือ exclusive-OR และ exclusive-NOR

            Ex-OR

            เป็นลอจิกเกตที่เอาต์พุตจะเป็น “1” เมื่ออินพุตมีลอจิกที่ต่างกัน นิพจน์ของ Ex-OR สามารถเขียนได้เป็น

วิธีทำ

เอาต์พุตของ Ex-OR สามารถสเก็ตได้จากความจริงที่ว่า เอาต์พุต จะเป็น “1” เมื่อ อินพุตมีลอจิกต่างกัน ผลลัพธืที่ได้มีจุดที่น่าสนใจดังนี้

1. รูปคลื่นของเอาต์พุต x จะเหมือนกับอินพุต A ในระหว่างที่ B = 0 (ในช่วงเวลา t₀  ถึง t₁ และ t₂ ถึง t₃)

2. รูปคลื่นของเอาต์พุต x จะตรงกันข้ามกับอินพุต A ในระหว่างที่ B = 1 (ในช่วงเวลา t₁ ถึง t₂)

3. จะสังเกตได้ว่า Ex-OR สามารถนำมาใช้เป็น นอตเกตที่ควบคุมได้ โดยอินพุตหนึ่งสามารถนำมาใช้ในการควบคุมขั้วของลอจิกของอีกอินพุตหนึ่งได้