พีชคณิตบูลีน

พีชคณิตบูลีน (Boolean ) เป็นเครื่องมือ ที่ช่วยในการวิเคราะห์และออกแบบระบบดิจิตอล พีชคณิตบูลีนทำให้เราสามารถอธิบายความสัมพันธ์ระหว่าง เอาต์พุตและอินพุตของลอจิกเกตในรูปของสมการพีชคณิตหรือ นิพจน์บูลีน (Boolean expression)

1. การอธิบายวงจรลอจิกในรูปพีชคณิต

วงจรลอจิกใดๆ ไม่ว่าจะมีความซับซ้อนมากเพียงใด เราก็สามารถจะอธิบายด้วยการดำเนินการบูลีนได้ เนื่องจากมีการดำเนินการ OR, AND และ NOT เป็นการดำเนินการพื้นฐานของระบบดิจิตอล ตัวอย่างในรูปที่ 1.1 แสดงการเขียนนิพจน์ที่ใช้แสดงความสัมพันธ์ระหว่าง เอาต์พุต x กับ อินพุต A, B และ C ของวงจรลอจิก จะเห็นได้ว่าแอนด์เกตทำการแอนด์ อินพุต Aและ B จากนั้นจึงถูกออร์กับ อินพุต C โดย ออร์เกต ได้ผลลัพธ์เป็นเอาต์พุต x ในที่สุด เพื่อไม่ให้เกิดความสับสน ในกรณีที่มีการออร์และแอนด์ในวงจรลอจิก จะกำหนดให้การดำเนินการแอนด์เกิดขึ้นก่อนการออร์ ยกเว้นหากมีการใส่วงเล็บกำหนดการดำเนินการไว้อย่างชัดเจน ซึ่งมีลักษณะคล้ายกับ อับดับของการดำเนินการทางพีชคณิตทั่วๆไป ที่จะทำการคูณตัวเลขก่อนทำการบวก รูปที่ 1.2 และ 1.3 แสดงตัวอย่างวงจรลอจิกและการเขียนนิพจน์ของวงจรลอจิกที่มีการดำเนินการออร์ก่อน แอนด์ และวงจรที่มีการใช้นอตเกตหรือ อินเวอร์เตอร์ ตามลำดับ รูปที่ 1.4 แสดงตัวอย่างวงจรลอจิกที่มีความซับซ้อน การใช้วงเล็บหลายแบบมาแยกการดำเนินการจะช่วยให้นิพจน์ดูง่ายไม่สับสน

2. การหาค่าเอาต์พุตของวงจรลอจิก

            เมื่อนิพจน์บูลีนของเอาต์พุตของวงจรลอจิกสามารถเขียนออกมาได้ การหาค่าเอาต์พุต สำหรับชุดอินพุตหนึ่งๆสามารถหาได้โดยการแทนค่าระดับลอจิก “0”, “1” ของอินพุตนั้นๆ ลงไปในตัวแปรภายในนิพจน์ ยกตัวอย่างการหาลอจิกเอาต์พุตของวงจรในรูปที่ 1.4 สำหรับกรณีที่อินพุตเป็น A = 0, B = 1, C = 1, D = 0 และ E = 1 จะได้ผลลัพธ์ดังนี้

กฎพื้นฐานในการแทนค่าในนิพจน์บูลีนมีดังนี้

1. แทนค่านิเสธในเทอมเดี่ยวให้หมดเสียก่อน 

2. แทนค่าภายในวงเล็บ

3. ดำเนินการแอนด์ก่อนการออร์ยกเว้นมีวงเล็บกำกับไว้

4. ถ้านิพจน์มีนิเสธคร่อมอยู่ให้ดำเนินการภายในนิพจน์ดังกล่าว แล้วจึงกลับผลลอจิก

            นอกจากนี้แล้ว เรายังสามารถหาค่าลอจิกเอาต์พุตของวงจรลอจิกได้โดยการแทนค่าลอจิกลงในวงจร ดังตัวอย่างในรูปที่ 2.1

3. การสร้างวงจรลอจิกจากนิพจน์บูลีน

            หากการดำเนินการของวงจรลอจิกเขียนอยู่ในรูปนิพจน์บูลีน เราสามารถนำมาสร้างวงจรลอจิกได้โดยตรง พิจารณานิพจน์ เราจะเห็นว่านิพจน์นี้ประกอบไปด้วยสามเทอม ที่ออร์กัน ดังนั้น เราต้องใช้ออร์เกตที่มีสามอินพุตมาใช้ในวงจร และอินพุตของออร์เกต ก็เป็นเทอมการแอนด์ ซึ่งนิยมเรียกว่า เทอมของผลคูณ (Product term) เราจะสามารถวาดรูปวงจรลอจิกสุดท้ายได้ดังรูปที่ 3.1

ในหัวข้อต่อๆไปเราจะได้ศึกษาถึงวิธีการออกแบบวงจรลอจิกที่ใช้จำนวนลอจิกเกตน้อยกว่าวิธีทางตรง แต่สามารถให้ผลของลอจิกเอาต์พุตที่เหมือนกัน

4. ทฤษฎีบทของบูลีน

            ที่ผ่านมาเราจะเห็นถึงประโยชน์ของการใช้พีชคณิตบูลีน ในการวิเคราะห์วงจรลอจิก และแทนการดำเนินการของวงจรลอจิกในรูปแบบนิพจน์คณิตศาสตร์ได้ ในหัวข้อนี้ เราจะได้เรียนรู้เกี่ยวกับทฤษฎีบทของบูลีนหรือ กฎของบูลีน ซึ่งจะสามารถช่วยให้เราลดรูปวงจรลอจิกให้มีขนาดเล็กลง ในที่นี้กำหนดให้ตัวแปร x เป็นตัวแปรบูลีนที่สามารถเป็นได้ทั้ง “0” และ “1” ในแต่ล่ะข้อจะมีรูปวงจรแสดงถึงการมีอยู่ของกฎนั้น

          1. ตัวแปร xใดๆ ถ้าแอนด์กับ “0” ผลลัพธ์ของลอจิก ต้องเป็น “0”

          2. ตัวแปร xใดๆ ถ้าแอนด์กับ “1” ผลลัพธ์ของลอจิก เท่ากับลอจิกของ x

          3. ตัวแปร xใดๆ ถ้าแอนด์กับตัวมันเอง ผลลัพธ์ของลอจิก เท่ากับลอจิกของ x พิสูจน์จาก หาก x = 0 ดังนั้น0 . 0 = 0 ; หาก 1 . 1 = 1 ดังนั้น

          4. ตัวแปร x ใด หากแอนด์กับคอมพลีเมนต์ของตัวมันเอง (  ) ผลลัพธ์ของลอจิกเป็น “0”

          5. ตัวแปร x ใดๆ หากออร์กับ “0” ผลลัพธ์ของลอจิกไม่เปลี่ยนแปลง

          6. ตัวแปร x ใดๆ หากออร์กับ “1” ผลลัพธ์ลอจิกต้องเป็น “1”

          7. ตัวแปร x ใดๆ หากออร์กับตัวมันเอง ผลลัพธ์ลอจิกเท่ากับลอจิกของ x

          8. ตัวแปร x ใดๆ หาก ออร์กับคอมพลีเมนต์ของตัวเอง ผลลัพธ์ลอจิกเท่ากับ “1”

ต่อไปนี้จะเป็นตัวอย่างการลดรูปโดยใช้ทฤษฎีบทของบูลีน เพื่อให้วงจรลอจิกใช้จำนวนเกตลดลง

5. ทฤษฎีบทของ ดีมอร์แกน

 ทฤษฎีบทที่สำคัญที่สุดสองข้อ ของทฤษฎีบทของบูลีน มาจากการคิดค้นของ นักคณิตศาสตร์เอกนามว่า ดีมอร์แกน (DeMorgan)

พิจารณา (17)

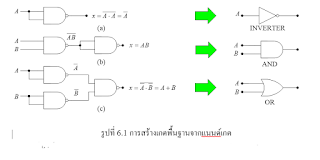
6. การสร้างลอจิกเกตต่างๆจาก แนนด์เกตและนอร์เกต

            ทุกนิพจน์ของบูลีนจะประกอบไปด้วยการผสมกันของการดำเนินการลอจิกแบบพื้นฐาน ออร์ แอนด์ และ นิเสธ ดังนั้นเราสามารถสร้างวงจรลอจิกโดยนำ ออร์เกต แอนด์เกต และอินเวอร์เตอร์เกต มาประกอบกันเป็นวงจรดิจิตอล แต่เราสามารถนำแนนด์เกตเพียงมาสร้างเป็นเกตต่างๆได้ ดังตัวอย่างในรูปที่ 6.1

วงจรลอจิกแบบคอมไบเนชั่น

ในหัวข้อที่ผ่านมา เราได้รู้จักถึงเกตพื้นฐานชนิดต่างๆ และ พีชคณิตของบูลีนที่ช่วยในการอธิบายการดำเนินการของวงจรให้อยู่ในรูปนิพจน์และวิเคราะห์การทำงานของวงจรที่สร้างจากวงจรลอจิกเกตหลายๆแบบมาต่อรวมกันหรือ เรียกว่าเป็นวงจรแบบคอมไบเนชั่น (Combination) วงจรคอมไบเนชั่น นี้ไม่มีลักษณะของความจำ (Memory) เอาต์พุตของวงจรคอมไบเนชั่น ขึ้นอยู่กับอินพุตในขณะนั้นๆ

1. ผลบวกของผลคูณ (Sum-of-Product)

            ในการลดรูปวงจรลอจิก เราจะต้องการเรียนรู้การเขียน นิพจน์ในรูปของผลบวกของผลคูณ

          

ความหมายของผลบวกของผลคูณคือ เทอมของการแอนด์หลายๆเทอม ออร์กัน โดยที่เทอมแอนด์แต่ล่ะเทอมอาจมีตัวแปรอยู่ในรูปคอมพลีเมนต์หรือ อยู่ในรูปที่ไม่เป็นคอมพลีเมนต์ (ไม่กลับผลลอจิก) เพียงเท่านั้น

 หมายเหตุจะไม่เครื่องหมายนิเสธครอบบนตัวแปรมากกว่าหนึ่งตัว (เช่นหรือเป็นต้น )         

2. ผลคูณของผลบวก (Product-of-Sum)

            รูปแบบทั่วไปอีกชนิดหนึ่งคือ ผลคูณของผลบวก ที่ประกอบไปด้วยเทอมออร์หลายๆเทอม แอนด์กันอยู่

ในการลดรูปเราสามารถใช้นิพจน์ในรูปผลบวกของผลคูณแต่เพียงอย่างเดียวได้ ดังนั้น จะไม่กล่าวถึงการลดรูปโดยการใช้รูปผลคูณของผลบวก

3. การลดรูปวงจรลอจิก

            เมื่อเราสามารถเขียนนอพจน์ของเอาต์พุตของวงจรลอจิกขึ้นมาได้ เราอาจจะสามารถลดรูปให้เป็นนิพจน์ใหม่ที่มีจำนวนเทอม หรือ จำนวนตัวแปรลดลง ซึ่งทำให้เราใช้จำนวนเกตที่ลดลงด้วย ทำให้วงจรมีขนาดเล็กลงและราคาถูกลง นอกจากนี้ความเชื่อมั่นของวงจรก็จะมีสูงขึ้นเนื่องจากมีจำนวนจุดต่อที่ลดลง

4. การลดรูปโดยวิธีทางพีชคณิต

            เราสามารถใช้ทฤษฎีบทของบูลีนในการลดรูปนิพจน์สำหรับสร้างวงจรลอจิก เป็นการยากที่จะระบุว่าควรใช้ทฤษฎีบทของบูลีนข้อใด ในการลดรูปนิพจน์ ให้อยู่ในรูปที่ง่ายที่สุด เพราะขึ้นอยู่กับการลองผิดลองถูกและความชำนาญของเฉพาะบุคคล ในตัวอย่างต่อไปจะแสดงวิธีการลดรูปนิพจน์หลายๆวิธี ซึ่งจะสังเกตได้ว่ามีขั้นตอนสำคัญๆ  2 ขั้นตอนคร่าวๆได้ดังนี้

1. ทำการแปลงนิพจน์ตั้งต้นให้อยู่ในรูปผลบวกของผลคูณ โดยใช้ทฤษฎีบทของ ดีมอร์แกนและการคูณเทอม

2. เมื่อสามารถแปลงให้อยู่ในรูปของผลบวกของผลคูณได้แล้ว จึงพิจารณาหาเทอมที่มีร่วมกัน แล้วทำการดึงเทอมร่วมนั้นออกมา เพื่อหวังให้จำนวนเทอมลดลง

ตัวอย่าง จงลดรูปวงจรลอจิกต่อไปนี้

วิธีทำ

ขั้นตอนแรกให้หานิพจน์ของเอาต์พุต z ของวงจรลอจิก

ผลลัพธ์ที่ได้นี้เมื่อนำมาสร้างเป็นวงจรลอจิกในรูปที่ 4.1(b) จะเห็นได้ว่ารูปวงจรมีความซับซ้อนน้อยลงเป็นอย่างมาก

5. การออกแบบวงจรลอจิกคอมไบเนชั่นจากตารางความจริง

            ตัวอย่าง5.1 จงออกแบบวงจรลอจิกที่มีตารางความจริง ในตารางที่ 5.1

6. การลดรูปวงจรโดยการใช้ Karnaugh Map

            Karnaugh map เป็นวิธีทางภาพที่ใช้ในการลดรูปสมการลอจิก ในทางปฎิบัติ สามารถใช้กับตัวแปรบูลีนได้สูงสุด 6 ตัวแปร สำหรับการสร้างตารางด้วยมือจะจำกัดที่ 4 ตัวแปร

ตัวอย่างตารางสำหรับ 2 ตัวแปร 3 ตัวแปร และ 4 ตัวแปร แสดงไว้ในรูปที่ 6.1

การจับคู่เทอมที่เหมือนกัน สามารถทำได้โดยการวงรอบเทอมที่อยู่ติดกัน เป็นแบบ 2 เทอม 4 เทอม และ 8 เทอม โดยเทอมที่ตัวแปรในรูปคอมพลีเมนต์และรูปปกติจะถูกยุบไป

6.1 วงรอบ 2 เทอม

พิจารณาตัวอย่างการวงรอบเทอมที่อยู่ติดกันสองเทอม

7. Exclusive-OR และ Exclusive-NOR

            วงจรลอจิกเกตแบบพิเศษที่นิยมใช้ในระบบดิจิตอลคือ exclusive-OR และ exclusive-NOR

            Ex-OR

            เป็นลอจิกเกตที่เอาต์พุตจะเป็น “1” เมื่ออินพุตมีลอจิกที่ต่างกัน นิพจน์ของ Ex-OR สามารถเขียนได้เป็น

วิธีทำ

เอาต์พุตของ Ex-OR สามารถสเก็ตได้จากความจริงที่ว่า เอาต์พุต จะเป็น “1” เมื่อ อินพุตมีลอจิกต่างกัน ผลลัพธืที่ได้มีจุดที่น่าสนใจดังนี้

1. รูปคลื่นของเอาต์พุต x จะเหมือนกับอินพุต A ในระหว่างที่ B = 0 (ในช่วงเวลา t₀  ถึง t₁ และ t₂ ถึง t₃)

2. รูปคลื่นของเอาต์พุต x จะตรงกันข้ามกับอินพุต A ในระหว่างที่ B = 1 (ในช่วงเวลา t₁ ถึง t₂)

3. จะสังเกตได้ว่า Ex-OR สามารถนำมาใช้เป็น นอตเกตที่ควบคุมได้ โดยอินพุตหนึ่งสามารถนำมาใช้ในการควบคุมขั้วของลอจิกของอีกอินพุตหนึ่งได้

สรุป